Don't worry be Nyu'ng
Pendahuluan ke Teorema Pythagoras
Rumus Pythagoras merupakan salah satu konsep dasar dalam matematika yang ditemukan oleh seorang filsuf dan matematikawan Yunani kuno, Pythagoras. Pythagoras, yang hidup pada sekitar abad ke-6 SM, terkenal karena kontribusinya yang luas dalam bidang matematika, terutama dalam pengembangan teorema yang kini menyandang namanya. Teorema ini berkaitan dengan geometri segitiga siku-siku dan menyatakan bahwa dalam sebuah segitiga siku-siku, kuadrat panjang hipotenusa (sisi miring) sama dengan jumlah kuadrat panjang kedua sisi lainnya.
Secara matematis, teorema Pythagoras dapat dinyatakan dengan rumus: a2 + b2 = c2, di mana c adalah panjang hipotenusa, dan a serta b adalah panjang kedua sisi lainnya. Teorema ini sangat penting karena memberikan cara yang sederhana dan efektif untuk menghitung panjang sisi yang tidak diketahui dalam segitiga siku-siku, hanya dengan mengetahui panjang dua sisi lainnya. Hal ini membuat teorema Pythagoras menjadi alat yang sangat berguna dalam berbagai aplikasi praktis, seperti teknik sipil, arsitektur, dan navigasi.
Selain aplikasinya yang luas, teorema Pythagoras juga memiliki nilai pendidikan yang tinggi. Memahami konsep ini membantu siswa mengembangkan keterampilan berpikir logis dan analitis, serta memperkuat pemahaman mereka tentang hubungan antara berbagai elemen dalam geometri. Penguasaan teorema ini juga menjadi dasar bagi banyak konsep matematika yang lebih kompleks dan lanjutan.
Oleh karena itu, teorema Pythagoras tidak hanya penting sebagai konsep matematika dasar tetapi juga sebagai fondasi untuk pemahaman yang lebih mendalam dalam ilmu pengetahuan dan teknik. Dengan mengenal sejarah Pythagoras dan memahami esensi teorema ini, pembaca akan lebih siap untuk mengeksplorasi penerapan praktis dan teoretis dari rumus Pythagoras dalam kehidupan sehari-hari.
Rumus Pythagoras Dasar
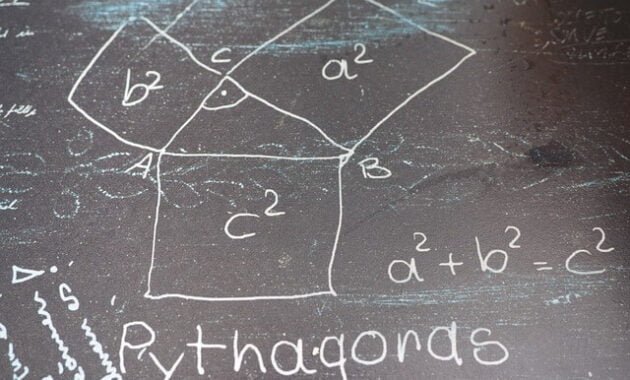
Rumus dasar Pythagoras adalah salah satu konsep fundamental dalam matematika, terutama dalam geometri. Rumus ini dinyatakan dalam bentuk a² + b² = c², di mana a dan b adalah panjang dua sisi segitiga siku-siku yang membentuk sudut 90 derajat, sementara c adalah panjang sisi miring atau hipotenusa. Hipotenusa adalah sisi terpanjang dalam segitiga siku-siku dan berseberangan dengan sudut siku-siku tersebut.
Untuk lebih memahami penerapan rumus Pythagoras, mari kita lihat contoh sederhana. Misalkan kita memiliki sebuah segitiga siku-siku dengan panjang sisi a = 3 cm dan sisi b = 4 cm. Menurut rumus Pythagoras, kita dapat menghitung panjang sisi c dengan cara sebagai berikut:
a² + b² = c²
3² + 4² = c²
9 + 16 = c²
25 = c²
c = √25
c = 5 cm
Dari perhitungan di atas, kita menemukan bahwa panjang sisi miring segitiga tersebut adalah 5 cm. Dengan demikian, rumus Pythagoras memudahkan kita untuk menentukan panjang salah satu sisi segitiga jika panjang dua sisi lainnya diketahui. Hal ini sangat berguna dalam berbagai aplikasi, termasuk dalam pemecahan masalah sehari-hari serta dalam berbagai bidang ilmu pengetahuan dan teknik.
Rumus Pythagoras tidak hanya terbatas pada segitiga siku-siku yang memiliki panjang sisi bilangan bulat, tetapi juga berlaku untuk semua segitiga siku-siku, termasuk yang memiliki panjang sisi dalam bentuk desimal atau pecahan. Pemahaman yang mendalam tentang rumus ini akan membantu kita dalam menguasai lebih banyak konsep dalam geometri dan matematika secara umum.
Aplikasi Rumus Pythagoras dalam Kehidupan Sehari-hari
Rumus Pythagoras, yang terkenal dalam dunia matematika, memiliki banyak aplikasi praktis dalam kehidupan sehari-hari. Salah satu penggunaan yang paling umum adalah dalam bidang geometri, khususnya dalam menghitung jarak antara dua titik pada peta. Misalkan, jika seseorang ingin mengetahui jarak langsung dari satu titik ke titik lainnya yang berjarak horizontal dan vertikal tertentu, rumus Pythagoras dapat memberikan solusi cepat dan akurat. Misalnya, jika seorang pendaki ingin mengetahui jarak langsung antara dua titik pada peta yang berjarak 3 km ke timur dan 4 km ke utara, rumus Pythagoras dapat digunakan untuk menentukan bahwa jaraknya adalah 5 km.
Selain itu, rumus Pythagoras juga sangat berguna dalam dunia konstruksi dan arsitektur. Misalnya, untuk menentukan panjang tangga yang diperlukan untuk mencapai ketinggian tertentu. Jika seorang pekerja konstruksi perlu memasang tangga untuk mencapai ketinggian 6 meter, dan jarak horizontal dari dasar tangga ke dinding adalah 8 meter, maka panjang tangga dapat dihitung menggunakan rumus Pythagoras. Dalam hal ini, panjang tangga tersebut adalah 10 meter, yang merupakan hasil dari akar kuadrat dari jumlah kuadrat tinggi dan jarak horizontal.
Contoh lain dari aplikasi rumus Pythagoras adalah dalam navigasi dan teknologi GPS. Sistem ini sering kali menggunakan prinsip-prinsip dasar geometri untuk menentukan posisi dan jarak antara dua titik di permukaan bumi. Ketika dua koordinat geografis diketahui, rumus Pythagoras dapat digunakan untuk menghitung jarak lurus antara dua lokasi tersebut, memudahkan navigasi dan perencanaan perjalanan.
Rumus Pythagoras juga dapat diterapkan dalam olahraga, misalnya dalam menentukan jarak tembakan atau pukulan dalam permainan bola basket atau golf. Dengan demikian, aplikasi rumus Pythagoras dalam kehidupan sehari-hari sangat luas dan bervariasi, memberikan solusi praktis dan efisien dalam berbagai situasi.
Contoh Soal dan Penyelesaian
Untuk memahami lebih dalam mengenai penggunaan rumus Pythagoras, berikut beberapa contoh soal beserta langkah-langkah penyelesaiannya yang dapat membantu Anda. Rumus Pythagoras yang sering digunakan adalah a² + b² = c² di mana c adalah sisi miring dari segitiga siku-siku, dan a serta b adalah sisi-sisi lainnya.
Contoh Soal 1: Diketahui segitiga siku-siku dengan panjang sisi-sisi tegak lurus masing-masing 3 cm dan 4 cm. Cari panjang sisi miring (c).
Penyelesaian:
1. Tuliskan rumus Pythagoras: a² + b² = c²
2. Masukkan nilai-nilai yang diketahui: 3² + 4² = c²
3. Hitung nilai kuadrat dari sisi-sisi tegak lurus: 9 + 16 = c²
4. Jumlahkan kedua hasil tersebut: 25 = c²
5. Ambil akar kuadrat dari kedua sisi persamaan untuk mendapatkan nilai c: c = √25
6. Jadi, panjang sisi miring c adalah 5 cm.
Contoh Soal 2: Diketahui segitiga siku-siku dengan panjang sisi miring 13 cm dan salah satu sisi tegak lurus 5 cm. Cari panjang sisi tegak lurus lainnya (b).
Penyelesaian:
1. Tuliskan rumus Pythagoras: a² + b² = c²
2. Masukkan nilai-nilai yang diketahui: 5² + b² = 13²
3. Hitung nilai kuadrat dari sisi yang diketahui: 25 + b² = 169
4. Kurangkan 25 dari kedua sisi persamaan untuk mendapatkan nilai b²: b² = 144
5. Ambil akar kuadrat dari kedua sisi persamaan untuk mendapatkan nilai b: b = √144
6. Jadi, panjang sisi tegak lurus lainnya b adalah 12 cm.
Dengan contoh-contoh di atas, diharapkan Anda lebih memahami cara menerapkan rumus Pythagoras dalam penyelesaian masalah matematika sehari-hari. Memahami langkah-langkah ini dengan baik akan sangat berguna dalam berbagai aspek kehidupan, terutama dalam bidang yang banyak menggunakan prinsip-prinsip geometris.
Kesalahan Umum dalam Menggunakan Rumus Pythagoras
Saat mempelajari rumus Pythagoras, siswa sering kali melakukan beberapa kesalahan yang bisa mengakibatkan hasil yang tidak akurat. Salah satu kesalahan umum adalah salah menentukan sisi mana yang merupakan hipotenusa. Dalam segitiga siku-siku, hipotenusa adalah sisi terpanjang yang berhadapan langsung dengan sudut siku-siku. Sering kali, siswa mengira salah satu dari dua sisi lainnya sebagai hipotenusa, yang dapat mengganggu perhitungan mereka.
Kesalahan lain yang sering terjadi adalah salah dalam mengidentifikasi segitiga siku-siku. Rumus Pythagoras hanya berlaku untuk segitiga yang memiliki satu sudut 90 derajat. Menggunakan rumus ini pada segitiga yang tidak memenuhi kriteria tersebut akan menghasilkan perhitungan yang tidak akurat. Oleh karena itu, penting bagi siswa untuk memastikan bahwa mereka benar-benar bekerja dengan segitiga siku-siku sebelum menerapkan rumus Pythagoras.
Selain itu, kesalahan dalam melakukan perhitungan aritmetika juga sering menjadi kendala. Kesalahan dalam penghitungan kuadrat dari sisi atau dalam penjumlahan dan pengurangan bisa menyebabkan hasil yang salah. Siswa harus berhati-hati dan memeriksa kembali perhitungan mereka untuk memastikan bahwa semua langkah dilakukan dengan benar.
Untuk menghindari kesalahan-kesalahan ini, beberapa tips yang bisa diikuti oleh siswa antara lain:
1. Selalu identifikasi sisi hipotenusa terlebih dahulu. Ingat bahwa hipotenusa adalah sisi yang berhadapan langsung dengan sudut siku-siku dan merupakan sisi terpanjang dalam segitiga.
2. Pastikan segitiga yang digunakan adalah segitiga siku-siku. Cek sudut-sudut segitiga untuk memastikan salah satunya adalah 90 derajat.
3. Lakukan perhitungan aritmetika dengan hati-hati. Periksa kembali setiap langkah perhitungan untuk menghindari kesalahan dasar dalam penghitungan kuadrat atau operasi lainnya.
Dengan memperhatikan hal-hal di atas, siswa dapat mengurangi kemungkinan melakukan kesalahan saat menggunakan rumus Pythagoras dan mendapatkan hasil yang lebih akurat dalam perhitungan mereka.
Variasi dari Teorema Pythagoras
Teorema Pythagoras, yang biasanya dikenal dalam konteks geometri dua dimensi, juga memiliki variasi yang berlaku dalam geometri tiga dimensi. Salah satu variasi yang kurang dikenal adalah teorema Pythagoras dalam ruang tiga dimensi. Pada dasarnya, teorema ini dapat digunakan untuk menghitung panjang diagonal ruang dalam sebuah kubus atau balok.
Dalam ruang tiga dimensi, jika kita memiliki balok dengan panjang, lebar, dan tinggi masing-masing adalah a, b, dan c, maka panjang diagonal ruang d dapat dihitung menggunakan rumus:
d = √(a² + b² + c²)
Rumus ini adalah perluasan dari teorema Pythagoras yang menggabungkan tiga dimensi. Sebagai contoh, bayangkan kita memiliki sebuah kotak dengan panjang 3 cm, lebar 4 cm, dan tinggi 5 cm. Untuk menghitung panjang diagonal ruang kotak tersebut, kita bisa menggunakan rumus di atas:
d = √(3² + 4² + 5²) = √(9 + 16 + 25) = √50 ≈ 7,07 cm
Variasi lain dari teorema Pythagoras ditemukan dalam geometri analitis dan ruang Euclidean. Selain itu, konsep ini juga dapat diterapkan pada bidang yang lebih abstrak, seperti dalam analisis vektor dan ruang vektor. Dalam konteks ini, teorema Pythagoras membantu dalam menentukan jarak antara dua titik dalam ruang tiga dimensi, atau bahkan dalam ruang dengan dimensi yang lebih tinggi.
Dalam aplikasi praktis, variasi teorema Pythagoras sangat berguna dalam berbagai bidang, termasuk arsitektur, teknik sipil, dan ilmu komputer. Misalnya, dalam arsitektur, memahami panjang diagonal ruang suatu bangunan dapat membantu dalam perencanaan dan desain struktur. Sedangkan dalam ilmu komputer, konsep ini dapat digunakan dalam algoritma untuk menghitung jarak dalam ruang multidimensi.
Dengan memahami dan menguasai variasi dari teorema Pythagoras, kita dapat lebih mudah menyelesaikan masalah yang melibatkan geometri dalam kehidupan sehari-hari serta dalam bidang profesional tertentu. Teorema ini tidak hanya terbatas pada aplikasi sederhana, tetapi juga memiliki penerapan yang luas di berbagai disiplin ilmu.
Latihan Soal untuk Pemahaman Lebih Lanjut
Memahami konsep dasar rumus Pythagoras merupakan langkah awal yang penting dalam menguasai topik ini. Untuk membantu memperdalam pemahaman dan menguji kemampuan Anda, berikut ini adalah beberapa latihan soal yang mencakup berbagai tingkat kesulitan. Latihan-latihan ini dirancang untuk memberikan tantangan yang bervariasi, mulai dari yang sederhana hingga yang lebih kompleks.
Soal 1: Sebuah segitiga siku-siku memiliki panjang sisi-sisi yang berdekatan masing-masing 3 cm dan 4 cm. Hitung panjang sisi miringnya.
Soal 2: Pada sebuah segitiga siku-siku lainnya, panjang sisi miringnya adalah 13 cm dan salah satu sisi yang berdekatan adalah 5 cm. Temukan panjang sisi yang lainnya.
Soal 3: Sebuah tangga disandarkan pada dinding dengan ujung bawahnya berjarak 6 meter dari dinding. Jika panjang tangga tersebut adalah 10 meter, berapa ketinggian tangga tersebut mencapai dinding?
Soal 4: Dalam sebuah segitiga siku-siku, sisi miringnya berukuran 15 cm dan salah satu sisi yang berdekatan berukuran 9 cm. Hitung panjang sisi lainnya.
Soal 5: Sebuah taman berbentuk segitiga siku-siku dengan sisi-sisi yang berdekatan masing-masing berukuran 8 meter dan 15 meter. Tentukan panjang pagar yang dibutuhkan untuk menutupi seluruh keliling taman tersebut.
Latihan soal-soal ini dirancang untuk memberikan pemahaman lebih lanjut tentang penerapan rumus Pythagoras dalam berbagai situasi praktis. Dengan mengerjakan soal-soal ini, pembaca dapat menguji kemampuan mereka secara mandiri dan mengidentifikasi area yang mungkin memerlukan lebih banyak latihan. Selain itu, mencoba berbagai tingkat kesulitan akan membantu dalam memperkuat konsep dan meningkatkan keterampilan problem-solving secara keseluruhan.
Kesimpulan dan Rekomendasi Sumber Belajar Tambahan
Dalam artikel ini, kita telah membahas secara mendalam tentang rumus Pythagoras, yang merupakan salah satu konsep dasar dalam matematika. Teorema ini menyatakan bahwa dalam sebuah segitiga siku-siku, kuadrat panjang sisi miring (hipotenusa) sama dengan jumlah kuadrat panjang kedua sisi lainnya. Rumus ini sangat berguna dalam berbagai aplikasi praktis, baik dalam ilmu pengetahuan maupun kehidupan sehari-hari.
Pemahaman yang mendalam tentang rumus Pythagoras dapat mempermudah proses belajar matematika, terutama dalam topik-topik yang lebih kompleks seperti trigonometri dan geometri. Selain itu, menguasai teorema Pythagoras juga dapat meningkatkan keterampilan pemecahan masalah dan berpikir kritis.
Untuk membantu pembaca lebih memahami dan menguasai teorema Pythagoras, berikut adalah beberapa rekomendasi sumber belajar tambahan yang dapat dijadikan referensi:
Buku: “The Pythagorean Theorem: A Journey through Space and Time” oleh Alfred S. Posamentier dan Ingmar Lehmann menawarkan penjelasan lengkap dan berbagai aplikasi dari teorema Pythagoras. Buku ini cocok untuk pembaca yang ingin mendalami konsep ini lebih lanjut.
Video Tutorial: Saluran YouTube seperti “Khan Academy” menyediakan video tutorial yang mudah diikuti tentang teorema Pythagoras. Video-video ini menjelaskan konsep dasar, contoh soal, dan aplikasi praktis dengan cara yang interaktif dan mudah dipahami.
Website: Situs web “MathIsFun.com” memiliki berbagai artikel dan latihan soal interaktif yang dapat membantu memperkuat pemahaman tentang rumus Pythagoras. Situs ini juga menawarkan penjelasan visual dan animasi yang menarik.
Dengan memanfaatkan sumber-sumber belajar tambahan ini, diharapkan pembaca dapat lebih memahami dan menguasai teorema Pythagoras dengan baik. Pembelajaran yang berkelanjutan dan eksplorasi berbagai sumber akan sangat berguna dalam memperdalam pengetahuan matematika.




